Simulation of a Stochastic Model for the AKAP79 reaction network
simAKAP79stochastic.Rmd
require(SBtabVFGEN)
#> Loading required package: SBtabVFGEN
library(uqsa)
library(GillespieSSA2)This article provides code to simulate the AKAP79 stochastic model (one time, no sampling). We are plotting the model with default parameters which are not expected to fit the data (this is the starting point).
The Stochastic Model
When the copy number of molecular species in a reaction network system (AKAP79 in our case) is low, we cannot model the amount of molecules deterministically (e.g., with an ODE model), because the stochasticity in the reactions that take place cannot be ignored. In particular, the time at which reactions take place is random, as well as the specific reactions that take place (i.e., what pair of molecules react). To model such system we can use the master equation: we model the (integer) number of each molecule species in the system (e.g., proteins) and how the number of each molecule type (randomly) evolves in time. The likelihood of this model is hard to compute; however, we can easily sample trajectories from this stochastic model using the Gillespie algorithm. Given the current amount of each molecular species in the system at a given time point, we can sample the time at which the next reaction takes place and we can sample the type of reaction (i.e., what pair of molecules react).
To obtain the stochastic model for the reaction network, we need to compute the reaction propensities. These can be related to the reaction rate coefficients, that are the parameters that we usually use in our models, and on which we perform uncertainty quantification. To derive the reaction propensities we referred to this article.
Load the Model
This model is included with the package. To load your own model, see the article “Build and simulate your own Model”.
modelFiles <- uqsa_example("AKAP79",full.names=TRUE)
SBtab <- SBtabVFGEN::sbtab_from_tsv(modelFiles)
#> [tsv] file[1] «AKAP79_Compound.tsv» belongs to Document «AKAP79»
#> I'll take this as the Model Name.
#> AKAP79_Compound.tsv AKAP79_Experiments.tsv AKAP79_Expression.tsv AKAP79_Input.tsv AKAP79_Output.tsv AKAP79_Parameter.tsv AKAP79_Reaction.tsv X0uM_cAMPCaN_AKAP79_0_nM_cAMP.tsv X0uM_cAMPCaN_only_0_nM_cAMP.tsv X0uM_cAMPno_CaN_0_nM_cAMP.tsv X1000nM_cAMPCaN_AKAP79_1_uM_cAMP.tsv X1000nM_cAMPCaN_only_1_uM_cAMP.tsv X1000nM_cAMPno_CaN_1_uM_cAMP.tsv X100nM_cAMPCaN_AKAP79_100_nM_cAMP.tsv X100nM_cAMPCaN_only_100_nM_cAMP.tsv X100nM_cAMPno_CaN_100_nM_cAMP.tsv X2000nM_cAMPCaN_AKAP79_2_uM_cAMP.tsv X2000nM_cAMPCaN_only_2_uM_cAMP.tsv X2000nM_cAMPno_CaN_2_uM_cAMP.tsv X200nM_cAMPCaN_AKAP79_200_nM_cAMP.tsv X200nM_cAMPCaN_only_200_nM_cAMP.tsv X200nM_cAMPno_CaN_200_nM_cAMP.tsv X500nM_cAMPCaN_AKAP79_500_nM_cAMP.tsv X500nM_cAMPCaN_only_500_nM_cAMP.tsv X500nM_cAMPno_CaN_500_nM_cAMP.tsv
modelName <- checkModel("AKAP79",uqsa_example("AKAP79",pat="_gvf[.]c$"))
#> building a shared library from c source, and using GSL odeiv2 as backend (pkg-config is used here).
#> cc -shared -fPIC `pkg-config --cflags gsl` -o './AKAP79.so' '/tmp/Rtmp3XbkUp/temp_libpath315eec67fa214d/uqsa/extdata/AKAP79/AKAP79_gvf.c' `pkg-config --libs gsl`
comment(modelName)
#> [1] "./AKAP79.so"
# model related functions, in R, e.g. AKAP79_default() parameters
source(uqsa_example("AKAP79",pat='^AKAP79[.]R$'))
print(AKAP79_default())
#> kf_Rii_C__RiiP_C kf_RiiP_CxcAMP__RiiP_C_cAMP
#> 33.00000 0.49600
#> kf_RiiP_cAMPxC__RiiP_C_cAMP kb_RiiP_cAMPxC__RiiP_C_cAMP
#> 0.00545 0.01560
#> kb_RiiPXcAMP__RiiP_cAMP kf_RiiPXcAMP__RiiP_cAMP
#> 0.00160 0.01500
#> kf_RiiPxC__RiiP_C kb_RiiPxC__RiiP_C
#> 0.03800 0.00260
#> kf_cAMPxRii__Rii_cAMP kb_cAMPxRii__Rii_cAMP
#> 0.01500 0.00160
#> kf_Rii_CxcAMP__Rii_C_cAMP kb_Rii_CxcAMP__Rii_C_cAMP
#> 0.49600 1.41300
#> kf_RiixC__Rii_C kf_Rii_cAMPxC__Rii_C_cAMP
#> 2.10000 0.29840
#> kb_Rii_cAMPxC__Rii_C_cAMP kf_Rii_C_cAMP__RiiP_C_cAMP
#> 0.01800 33.00000
#> kb_RiixC__Rii_C AKAPoff_1
#> 0.00030 2.60000
#> AKAPoff_3 AKAPon_1
#> 20.00000 0.45000
#> AKAPon_3 kf_C_AKAR4
#> 2.00000 0.01800
#> kb_C_AKAR4 kcat_AKARp
#> 0.10600 10.20000
#> kmOFF kmON
#> 100.00000 1.00000
#> KD_T b_AKAP
#> 0.70000 0.00000Load Experiments (data)
experiments <- sbtab.data(SBtab)
# for example, these are the input and initial state of experiment 1:
print(experiments[[1]]$input)
#> [1] 1
print(experiments[[1]]$initialState)
#> Rii cAMP RiiP Rii_C RiiP_cAMP
#> 6.30 0.00 0.00 0.63 0.00
#> RiiP_C RiiP_C_cAMP C Rii_cAMP Rii_C_cAMP
#> 0.00 0.00 0.00 0.00 0.00
#> CaN RiiP_CaN RiiP_cAMP_CaN AKAR4 AKAR4_C
#> 1.50 0.00 0.00 0.20 0.00
#> AKAR4p
#> 0.00
# pick parameters for simulation
nInput <- length(experiments[[1]]$input)Here, we set parameters that we obtained as a result of uncertainty quantification as the default parameters don’t produce a good fit, they are still not optimal:
p <- 10^c(3.38,-0.22,-0.39,0.0013,7.89e-2,-1.02,-1.08,-2.86,-0.53,-0.34,-0.51,-2.42,-1.05,-1.37,-1.29,2.08,-2.79,-0.87,0.26,-0.168,-0.331,-1.77,-0.938,1.065,2.08,0.0147,-0.09893)
names(p) <- rownames(SBtab$Parameter)If instead we wanted to use the default parameters, then we could use this code:
p <- SBtabVFGEN::sbtab_quantity(SBtab$Parameter)Simulate
Function simulator.stoch will output a function
s, which will always simulate the scenarios described in
experiment e (i.e., same initial conditions, same inputs),
but for user supplied parameters.
exp_ind <- 9 #index of the experiment to consider
# generate a function (s) that simulates a trajectory given a parameter in input
ssa2 <- simulator.stoch(experiment = experiments, model.tab = SBtab, vol = 4e-16, outputFunction = AKAP79_func)
# simulate a trajectory (y) given parameter p
y <- ssa2(p)Simulation Results via ggplot2
require(ggplot2)
#> Loading required package: ggplot2
D<-data.frame(time=experiments[[exp_ind]]$outputTime,
AKAP79=experiments[[exp_ind]]$outputValues$AKAR4pOUT,
AKAP79ERR=experiments[[exp_ind]]$errorValues$AKAR4pOUT,
sim=y[[exp_ind]]$output)
ggplot(D) +
geom_linerange(mapping=aes(x=time,y=AKAP79,ymin=AKAP79-AKAP79ERR,ymax=AKAP79+AKAP79ERR),na.rm=TRUE) +
geom_point(mapping=aes(x=time,y=AKAP79),na.rm=TRUE) +
geom_line(mapping=aes(x=time,y=sim),color="purple",lwd=1.2)
#> Warning: Removed 125 rows containing missing values or values outside the scale range
#> (`geom_line()`).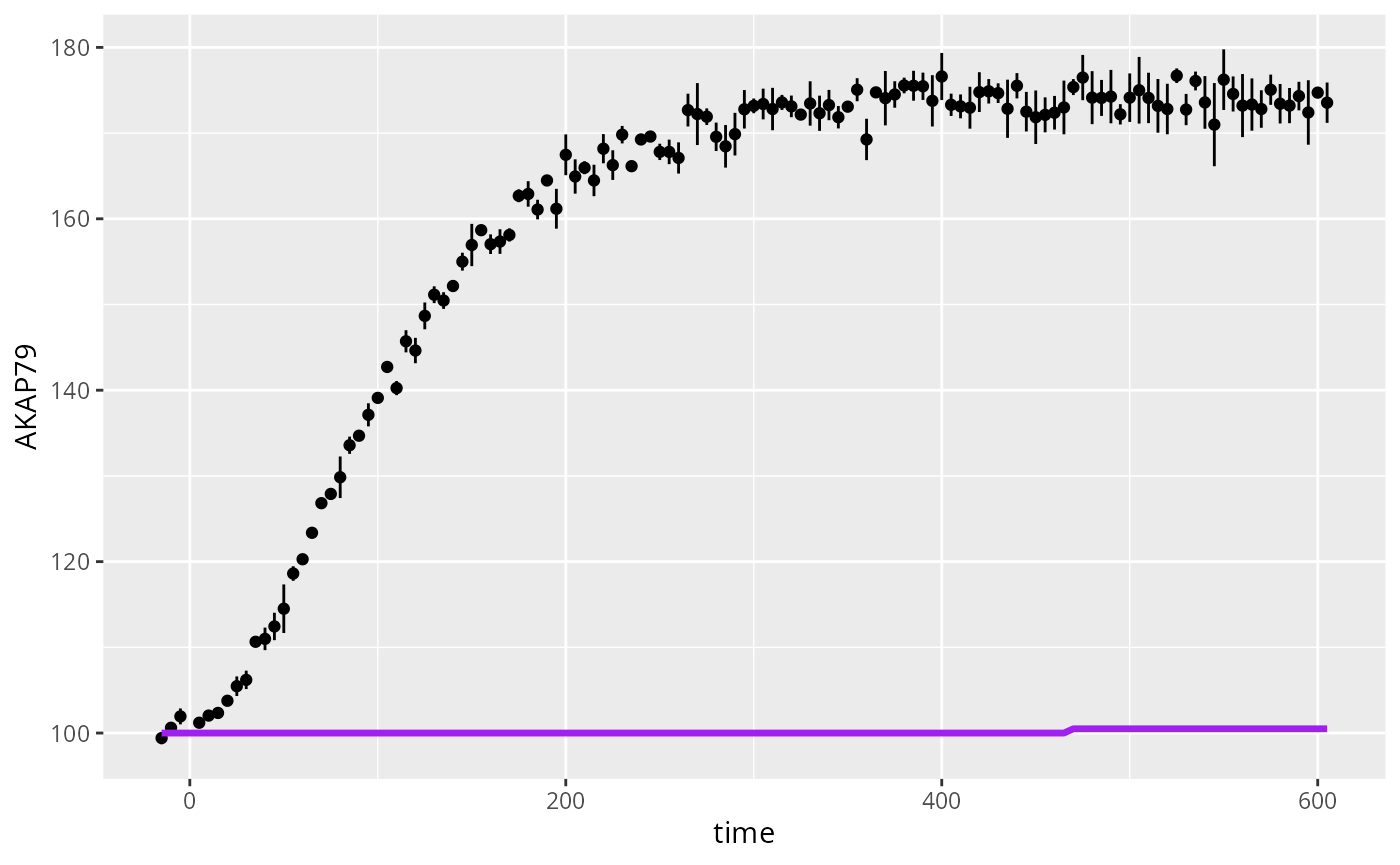
Built-in Stochastic simulator
Similarly, our built-in simulator uqsa::simstoch() can
be used to obtain a similar result:
C <- generateGillespieCode(SBtab)
cat(C,sep="\n",file="AKAP79_st.c")We compile that model to a shared library:
And next we simulate this compiled model:
P <- matrix(p,length(p),20)
st <- uqsa::simstoch(experiments,model.so="./akap79-st.so")
ystc <- st(P)And also get a reference simulation from the ODE solver:
sode <- uqsa::simcf(experiments,modelName)
yode <- sode(p)And also plot the results:
tm <- experiments[[exp_ind]]$outputTimes
ov <- experiments[[exp_ind]]$outputValues$AKAR4pOUT
ev <- experiments[[exp_ind]]$errorValues$AKAR4pOUT
par(bty="n")
plot(tm,ov,xlab="time",ylab="AKAR4p",main=names(experiments)[exp_ind],ylim=c(90,210))
arrows(tm,ov,tm,ov+ev,angle=90,length=0.02)
arrows(tm,ov,tm,ov-ev,angle=90,length=0.02)
for (j in seq(NCOL(P))){
lines(tm,as.numeric(ystc[[exp_ind]]$func["AKAR4pOUT",,j]),lwd=1,col="blue")
}
lines(tm,as.numeric(yode[[exp_ind]]$func["AKAR4pOUT",,1]),lwd=3)
Benchmark
Here we test which of the two simulates faster:
if (require(rbenchmark)){
BM <- benchmark(
GillespieSSA2 = {y1<-ssa2(p)},
uqsa = {y2 <- st(p)},
replications=10
)
}
#> Loading required package: rbenchmark
#> 84 0
#> [70,] 1 76 0 7 76 1
#> [71,] 0 94 0 10 94 1
#> [72,] 0 100 0 10 100 0
#> [73,] 0 94 0 9 94 0
#> [74,] 3 89 0 13 89 0
#> [75,] 0 88 0 6 88 0
#> [76,] 0 78 0 6 78 0
#> [77,] 2 89 0 15 89 1
#> [78,] 0 86 0 6 86 0
#> [79,] 1 81 0 13 81 1
#> [80,] 0 78 0 14 78 0
#> [81,] 0 83 0 7 83 0
#> [82,] 0 79 0 10 78 0
#> [83,] 1 72 0 18 73 0
#> [84,] 0 101 0 9 101 1
#> [85,] 2 89 0 10 89 0
#> [86,] 1 90 0 13 90 0
#> [87,] 1 85 0 11 85 1
#> [88,] 0 76 0 13 76 0
#> [89,] 0 97 0 7 97 0
#> [90,] 1 87 0 8 87 0
#> [91,] 1 106 0 8 106 0
#> [92,] 0 81 0 8 81 0
#> [93,] 1 75 0 4 75 0
#> [94,] 0 79 0 5 79 0
#> [95,] 0 99 0 7 99 0
#> [96,] 2 91 0 9 91 1
#> [97,] 2 87 0 11 87 0
#> [98,] 0 82 0 3 82 1
#> [99,] 1 87 0 14 87 0
#> [100,] 0 101 0 19 101 0
#> [101,] 2 90 0 5 90 0
#> [102,] 0 79 0 9 79 0
#> [103,] 1 89 0 13 89 0
#> [104,] 0 84 0 9 84 0
#> [105,] 2 84 0 12 84 0
#> [106,] 2 103 0 10 102 0
#> [107,] 0 82 0 8 83 0
#> [108,] 1 71 0 9 71 0
#> [109,] 0 88 0 8 88 0
#> [110,] 1 74 0 11 74 0
#> [111,] 2 97 0 8 97 0
#> [112,] 3 79 0 17 79 0
#> [113,] 3 81 0 13 81 0
#> [114,] 2 96 0 7 96 0
#> [115,] 1 75 0 11 75 0
#> [116,] 2 91 0 13 91 0
#> [117,] 3 89 0 9 89 0
#> [118,] 0 81 0 6 81 0
#> [119,] 0 85 0 8 85 0
#> [120,] 1 81 0 9 80 1
#> [121,] 1 83 0 12 84 1
#> [122,] 0 93 0 7 93 0
#> reaction26 reaction27
#> [1,] 0 0
#> [2,] 0 1
#> [3,] 0 0
#> [4,] 1 1
#> [5,] 0 1
#> [6,] 0 0
#> [7,] 0 0
#> [8,] 0 0
#> [9,] 0 0
#> [10,] 0 0
#> [11,] 0 1
#> [12,] 0 1
#> [13,] 0 1
#> [14,] 0 0
#> [15,] 0 0
#> [16,] 0 0
#> [17,] 0 0
#> [18,] 0 1
#> [19,] 0 1
#> [20,] 0 2
#> [21,] 0 0
#> [22,] 0 1
#> [23,] 0 0
#> [24,] 0 1
#> [25,] 0 0
#> [26,] 0 0
#> [27,] 0 0
#> [28,] 0 1
#> [29,] 0 1
#> [30,] 0 1
#> [31,] 0 1
#> [32,] 0 0
#> [33,] 1 0
#> [34,] 0 0
#> [35,] 0 0
#> [36,] 0 1
#> [37,] 0 1
#> [38,] 0 0
#> [39,] 0 0
#> [40,] 0 0
#> [41,] 0 2
#> [42,] 0 1
#> [43,] 0 0
#> [44,] 0 1
#> [45,] 0 1
#> [46,] 0 0
#> [47,] 0 0
#> [48,] 0 0
#> [49,] 0 2
#> [50,] 0 0
#> [51,] 0 1
#> [52,] 0 1
#> [53,] 0 1
#> [54,] 0 0
#> [55,] 0 0
#> [56,] 0 1
#> [57,] 0 0
#> [58,] 0 0
#> [59,] 0 1
#> [60,] 0 1
#> [61,] 0 0
#> [62,] 0 0
#> [63,] 0 0
#> [64,] 0 1
#> [65,] 0 0
#> [66,] 0 0
#> [67,] 0 0
#> [68,] 0 0
#> [69,] 0 0
#> [70,] 0 1
#> [71,] 0 0
#> [72,] 0 1
#> [73,] 0 0
#> [74,] 0 0
#> [75,] 0 0
#> [76,] 0 0
#> [77,] 0 1
#> [78,] 0 0
#> [79,] 0 1
#> [80,] 0 0
#> [81,] 0 0
#> [82,] 0 0
#> [83,] 0 0
#> [84,] 0 1
#> [85,] 0 0
#> [86,] 0 0
#> [87,] 0 1
#> [88,] 0 0
#> [89,] 0 0
#> [90,] 0 0
#> [91,] 0 0
#> [92,] 0 0
#> [93,] 0 0
#> [94,] 0 0
#> [95,] 0 0
#> [96,] 0 1
#> [97,] 0 0
#> [98,] 0 1
#> [99,] 0 0
#> [100,] 0 0
#> [101,] 0 0
#> [102,] 0 0
#> [103,] 0 0
#> [104,] 0 0
#> [105,] 0 0
#> [106,] 0 0
#> [107,] 0 0
#> [108,] 0 0
#> [109,] 0 0
#> [110,] 0 0
#> [111,] 0 0
#> [112,] 0 0
#> [113,] 0 0
#> [114,] 0 0
#> [115,] 0 0
#> [116,] 0 0
#> [117,] 0 0
#> [118,] 0 0
#> [119,] 0 0
#> [120,] 0 1
#> [121,] 0 1
#> [122,] 0 0
#>
#> $buffer
#> <0 x 0 matrix>
#>
#> $stats
#> method sim_name sim_time_exceeded all_zero_state negative_state
#> 1 exact NA TRUE FALSE FALSE
#> all_zero_propensity negative_propensity walltime_exceeded walltime_elapsed
#> 1 FALSE FALSE FALSE 0.6526881
#> num_steps dtime_mean dtime_sd firings_mean firings_sd
#> 1 183224 0.003302053 4.12663e-05 1 0
#>
#> attr(,"class")
#> [1] "ssa"
#> [1] 100.0000 101.4877 101.4877 102.9753 104.4630 104.4630 104.4630 104.4630
#> [9] 104.4630 104.4630 105.9507 107.4384 108.9260 108.9260 108.9260 108.9260
#> [17] 108.9260 110.4137 111.9014 114.8767 114.8767 116.3644 116.3644 117.8520
#> [25] 117.8520 117.8520 117.8520 119.3397 120.8274 122.3151 123.8027 123.8027
#> [33] 123.8027 123.8027 123.8027 125.2904 126.7781 126.7781 126.7781 126.7781
#> [41] 129.7534 131.2411 131.2411 132.7287 134.2164 134.2164 134.2164 134.2164
#> [49] 137.1918 137.1918 138.6794 140.1671 141.6548 141.6548 141.6548 143.1424
#> [57] 143.1424 143.1424 144.6301 146.1178 146.1178 146.1178 146.1178 147.6054
#> [65] 147.6054 147.6054 147.6054 147.6054 147.6054 149.0931 149.0931 150.5808
#> [73] 150.5808 150.5808 150.5808 150.5808 152.0685 152.0685 153.5561 153.5561
#> [81] 153.5561 153.5561 153.5561 155.0438 155.0438 155.0438 156.5315 156.5315
#> [89] 156.5315 156.5315 156.5315 156.5315 156.5315 156.5315 156.5315 158.0191
#> [97] 158.0191 159.5068 159.5068 159.5068 159.5068 159.5068 159.5068 159.5068
#> [105] 159.5068 159.5068 159.5068 159.5068 159.5068 159.5068 159.5068 159.5068
#> [113] 159.5068 159.5068 159.5068 159.5068 159.5068 159.5068 159.5068 160.9945
#> [121] 162.4821 162.4821
#> gs_mean firings_sd
#> 1 183483 0.00329731 6.062806e-06 1 0
#>
#> attr(,"class")
#> [1] "ssa"
#> [1] 100.0000 100.0000 100.0000 101.4877 101.4877 101.4877 101.4877 102.9753
#> [9] 105.9507 105.9507 105.9507 105.9507 107.4384 107.4384 110.4137 110.4137
#> [17] 110.4137 114.8767 114.8767 116.3644 116.3644 117.8520 117.8520 119.3397
#> [25] 120.8274 120.8274 120.8274 120.8274 122.3151 123.8027 125.2904 125.2904
#> [33] 125.2904 125.2904 126.7781 126.7781 126.7781 126.7781 126.7781 128.2657
#> [41] 129.7534 131.2411 131.2411 131.2411 131.2411 137.1918 137.1918 137.1918
#> [49] 137.1918 137.1918 137.1918 137.1918 140.1671 140.1671 140.1671 140.1671
#> [57] 140.1671 140.1671 140.1671 140.1671 140.1671 140.1671 140.1671 140.1671
#> [65] 140.1671 140.1671 140.1671 140.1671 140.1671 140.1671 140.1671 141.6548
#> [73] 141.6548 143.1424 144.6301 144.6301 144.6301 146.1178 146.1178 146.1178
#> [81] 149.0931 149.0931 149.0931 149.0931 149.0931 149.0931 149.0931 149.0931
#> [89] 150.5808 150.5808 150.5808 150.5808 150.5808 153.5561 153.5561 153.5561
#> [97] 153.5561 153.5561 153.5561 153.5561 153.5561 153.5561 153.5561 153.5561
#> [105] 155.0438 155.0438 155.0438 156.5315 156.5315 156.5315 156.5315 156.5315
#> [113] 158.0191 158.0191 158.0191 158.0191 159.5068 159.5068 159.5068 159.5068
#> [121] 159.5068 159.5068
#> 8 0 8 83 0 5
#> [104,] 4 0 5 90 0 10
#> [105,] 3 0 3 91 0 8
#> [106,] 4 0 4 89 0 12
#> [107,] 10 0 10 84 0 13
#> [108,] 7 0 7 86 0 7
#> [109,] 7 0 7 91 0 14
#> [110,] 12 0 12 90 0 15
#> [111,] 7 0 7 72 0 13
#> [112,] 3 0 3 77 0 5
#> [113,] 5 0 5 83 0 6
#> [114,] 6 0 6 88 0 13
#> [115,] 4 0 4 83 0 12
#> [116,] 9 0 9 92 0 15
#> [117,] 13 0 13 101 0 7
#> [118,] 5 0 5 80 0 8
#> [119,] 8 0 8 90 0 18
#> [120,] 6 0 6 81 0 8
#> [121,] 9 0 9 89 0 10
#> [122,] 7 0 7 81 0 5
#> reaction20 reaction21 reaction22 reaction23 reaction24 reaction25
#> [1,] 0 0 0 0 0 0
#> [2,] 1 89 0 11 89 0
#> [3,] 2 85 0 6 85 2
#> [4,] 0 95 0 9 95 0
#> [5,] 2 66 0 10 66 1
#> [6,] 0 81 0 10 81 1
#> [7,] 4 95 0 11 94 0
#> [8,] 0 79 0 8 80 2
#> [9,] 0 83 0 8 83 1
#> [10,] 0 75 1 8 73 0
#> [11,] 1 95 0 5 96 1
#> [12,] 3 87 0 14 87 0
#> [13,] 0 76 0 7 76 1
#> [14,] 1 93 0 6 93 0
#> [15,] 1 95 0 14 95 0
#> [16,] 0 87 1 12 86 1
#> [17,] 0 80 0 4 80 0
#> [18,] 0 86 0 11 86 0
#> [19,] 0 97 0 7 97 0
#> [20,] 0 76 0 4 76 0
#> [21,] 0 85 0 6 85 1
#> [22,] 0 87 0 11 87 0
#> [23,] 1 83 0 8 83 0
#> [24,] 0 80 0 8 80 2
#> [25,] 1 74 0 6 74 0
#> [26,] 0 91 0 10 91 1
#> [27,] 2 94 0 10 94 1
#> [28,] 0 85 0 10 85 1
#> [29,] 0 91 0 12 91 0
#> [30,] 0 102 0 6 102 0
#> [31,] 0 103 0 11 103 0
#> [32,] 0 91 0 7 91 0
#> [33,] 0 91 0 6 91 0
#> [34,] 3 79 0 15 78 1
#> [35,] 1 88 0 10 89 0
#> [36,] 1 85 0 10 85 0
#> [37,] 0 73 0 9 73 1
#> [38,] 1 80 0 15 80 0
#> [39,] 1 93 0 11 92 1
#> [40,] 0 86 0 16 87 1
#> [41,] 0 85 0 4 85 0
#> [42,] 1 98 0 7 98 1
#> [43,] 1 93 0 6 93 0
#> [44,] 0 74 0 11 74 0
#> [45,] 0 75 0 10 75 0
#> [46,] 1 83 0 11 83 0
#> [47,] 0 84 0 13 84 2
#> [48,] 0 92 0 15 92 0
#> [49,] 0 97 0 7 97 0
#> [50,] 0 99 0 8 99 0
#> [51,] 1 97 0 8 97 0
#> [52,] 4 84 0 13 84 0
#> [53,] 1 80 0 14 80 0
#> [54,] 1 85 0 16 85 0
#> [55,] 0 81 0 5 81 0
#> [56,] 1 77 0 8 77 0
#> [57,] 0 99 0 11 99 0
#> [58,] 0 78 0 13 78 0
#> [59,] 1 74 0 10 74 0
#> [60,] 0 90 0 8 90 1
#> [61,] 0 78 0 9 77 0
#> [62,] 0 95 0 8 96 0
#> [63,] 2 76 0 5 76 0
#> [64,] 2 83 0 14 83 0
#> [65,] 1 86 0 12 86 1
#> [66,] 0 91 0 8 91 1
#> [67,] 1 84 1 12 83 0
#> [68,] 2 98 0 6 98 0
#> [69,] 0 86 0 5 86 1
#> [70,] 2 99 0 13 99 1
#> [71,] 1 82 0 10 81 0
#> [72,] 1 82 0 10 83 0
#> [73,] 0 82 0 7 81 0
#> [74,] 2 93 0 13 94 0
#> [75,] 1 110 0 7 110 0
#> [76,] 1 98 0 6 98 0
#> [77,] 0 76 0 5 75 1
#> [78,] 0 90 0 6 91 1
#> [79,] 0 82 0 8 82 0
#> [80,] 2 92 0 10 92 1
#> [81,] 0 85 0 6 85 0
#> [82,] 0 82 0 12 82 0
#> [83,] 1 86 0 7 86 0
#> [84,] 1 84 0 5 84 0
#> [85,] 1 82 0 10 82 1
#> [86,] 2 77 0 10 77 1
#> [87,] 0 88 0 9 88 0
#> [88,] 1 80 0 11 80 0
#> [89,] 0 84 0 3 83 1
#> [90,] 0 95 0 5 96 0
#> [91,] 0 85 0 12 85 0
#> [92,] 0 101 0 4 100 2
#> [93,] 0 77 0 11 78 2
#> [94,] 2 101 0 5 100 0
#> [95,] 0 96 0 10 97 0
#> [96,] 0 96 0 11 96 0
#> [97,] 1 89 0 8 88 1
#> [98,] 1 90 0 7 91 0
#> [99,] 1 98 0 12 98 0
#> [100,] 1 96 0 13 96 0
#> [101,] 1 67 0 9 67 0
#> [102,] 0 72 0 9 72 0
#> [103,] 0 85 0 4 84 0
#> [104,] 2 87 0 8 87 0
#> [105,] 1 88 0 8 89 0
#> [106,] 0 80 0 12 80 0
#> [107,] 2 84 0 9 84 0
#> [108,] 0 84 0 8 84 0
#> [109,] 2 86 1 12 85 1
#> [110,] 0 89 0 16 89 0
#> [111,] 1 67 0 9 67 0
#> [112,] 1 76 0 7 76 0
#> [113,] 0 83 0 6 83 0
#> [114,] 2 83 0 11 83 0
#> [115,] 1 73 0 9 73 0
#> [116,] 0 88 0 14 87 0
#> [117,] 0 108 0 10 109 0
#> [118,] 1 78 0 7 78 0
#> [119,] 4 84 0 13 84 0
#> [120,] 0 79 0 8 78 0
#> [121,] 1 88 1 10 88 0
#> [122,] 0 84 0 4 84 1
#> reaction26 reaction27
#> [1,] 0 0
#> [2,] 0 0
#> [3,] 0 2
#> [4,] 0 0
#> [5,] 0 1
#> [6,] 0 1
#> [7,] 0 0
#> [8,] 0 2
#> [9,] 0 1
#> [10,] 0 0
#> [11,] 0 1
#> [12,] 0 0
#> [13,] 0 1
#> [14,] 0 0
#> [15,] 0 0
#> [16,] 0 1
#> [17,] 0 0
#> [18,] 0 0
#> [19,] 0 0
#> [20,] 0 0
#> [21,] 0 1
#> [22,] 0 0
#> [23,] 0 0
#> [24,] 0 2
#> [25,] 0 0
#> [26,] 0 1
#> [27,] 0 1
#> [28,] 0 1
#> [29,] 0 0
#> [30,] 0 0
#> [31,] 0 0
#> [32,] 0 0
#> [33,] 0 0
#> [34,] 0 1
#> [35,] 0 0
#> [36,] 0 0
#> [37,] 0 1
#> [38,] 0 0
#> [39,] 0 1
#> [40,] 0 1
#> [41,] 0 0
#> [42,] 0 1
#> [43,] 0 0
#> [44,] 0 0
#> [45,] 0 0
#> [46,] 0 0
#> [47,] 0 2
#> [48,] 0 0
#> [49,] 0 0
#> [50,] 0 0
#> [51,] 0 0
#> [52,] 0 0
#> [53,] 0 0
#> [54,] 0 0
#> [55,] 0 0
#> [56,] 0 0
#> [57,] 0 0
#> [58,] 0 0
#> [59,] 0 0
#> [60,] 0 1
#> [61,] 0 0
#> [62,] 0 0
#> [63,] 0 0
#> [64,] 0 0
#> [65,] 0 1
#> [66,] 0 1
#> [67,] 0 0
#> [68,] 0 0
#> [69,] 0 1
#> [70,] 0 1
#> [71,] 0 0
#> [72,] 0 0
#> [73,] 0 0
#> [74,] 0 0
#> [75,] 0 0
#> [76,] 0 0
#> [77,] 0 0
#> [78,] 0 2
#> [79,] 0 0
#> [80,] 0 1
#> [81,] 0 0
#> [82,] 0 0
#> [83,] 0 0
#> [84,] 0 0
#> [85,] 0 1
#> [86,] 0 1
#> [87,] 0 0
#> [88,] 0 0
#> [89,] 0 1
#> [90,] 0 0
#> [91,] 0 0
#> [92,] 0 2
#> [93,] 0 2
#> [94,] 0 0
#> [95,] 0 0
#> [96,] 0 0
#> [97,] 0 1
#> [98,] 0 0
#> [99,] 0 0
#> [100,] 0 0
#> [101,] 0 0
#> [102,] 0 0
#> [103,] 0 0
#> [104,] 0 0
#> [105,] 0 0
#> [106,] 0 0
#> [107,] 0 0
#> [108,] 0 0
#> [109,] 0 1
#> [110,] 0 0
#> [111,] 0 0
#> [112,] 0 0
#> [113,] 0 0
#> [114,] 0 0
#> [115,] 0 0
#> [116,] 0 0
#> [117,] 0 0
#> [118,] 0 0
#> [119,] 0 0
#> [120,] 0 0
#> [121,] 0 0
#> [122,] 0 1
#>
#> $buffer
#> <0 x 0 matrix>
#>
#> $stats
#> method sim_name sim_time_exceeded all_zero_state negative_state
#> 1 exact NA TRUE FALSE FALSE
#> all_zero_propensity negative_propensity walltime_exceeded walltime_elapsed
#> 1 FALSE FALSE FALSE 0.6593497
#> num_steps dtime_mean dtime_sd firings_mean firings_sd
#> 1 183790 0.003291832 9.429841e-06 1 0
#>
#> attr(,"class")
#> [1] "ssa"
#> [1] 100.0000 100.0000 102.9753 102.9753 104.4630 105.9507 105.9507 108.9260
#> [9] 110.4137 110.4137 111.9014 111.9014 113.3890 113.3890 113.3890 114.8767
#> [17] 114.8767 114.8767 114.8767 114.8767 116.3644 116.3644 116.3644 119.3397
#> [25] 119.3397 120.8274 122.3151 123.8027 123.8027 123.8027 123.8027 123.8027
#> [33] 123.8027 125.2904 125.2904 125.2904 126.7781 126.7781 128.2657 129.7534
#> [41] 129.7534 131.2411 131.2411 131.2411 131.2411 131.2411 134.2164 134.2164
#> [49] 134.2164 134.2164 134.2164 134.2164 134.2164 134.2164 134.2164 134.2164
#> [57] 134.2164 134.2164 134.2164 135.7041 135.7041 135.7041 135.7041 135.7041
#> [65] 137.1918 138.6794 138.6794 138.6794 140.1671 141.6548 141.6548 141.6548
#> [73] 141.6548 141.6548 141.6548 141.6548 141.6548 144.6301 144.6301 146.1178
#> [81] 146.1178 146.1178 146.1178 146.1178 147.6054 149.0931 149.0931 149.0931
#> [89] 150.5808 150.5808 150.5808 153.5561 156.5315 156.5315 156.5315 156.5315
#> [97] 158.0191 158.0191 158.0191 158.0191 158.0191 158.0191 158.0191 158.0191
#> [105] 158.0191 158.0191 158.0191 158.0191 159.5068 159.5068 159.5068 159.5068
#> [113] 159.5068 159.5068 159.5068 159.5068 159.5068 159.5068 159.5068 159.5068
#> [121] 159.5068 160.9945
print(BM)