Uncertainty Quantification and global Sensitivity Analysis on AKAR4 (deterministic)

library(uqsa)
library(SBtabVFGEN)
library(rgsl)

Load Model and Data

First we load the model and data, for detailed explanations see previous examples (Simulate AKAR4 deterministically).

f  <- uqsa::uqsa_example("AKAR4")
sb <- SBtabVFGEN::sbtab_from_tsv(f)
m  <- SBtabVFGEN::sbtab_to_vfgen(sb, cla=FALSE)
ex <- SBtabVFGEN::sbtab.data(sb)
C <- uqsa::generateCode(m)
cat(C,sep="\n",file="./AKAR4_gvf.c")
modelName <- checkModel("AKAR4",modelFile="./AKAR4_gvf.c")

Create simulator

We construct a simulator function and and test it on default parameter values.

s <- simcf(ex,modelName,parMap=log10ParMap) # or simulator.c
p <- log10(sb$Parameter[["!DefaultValue"]])
names(p) <- rownames(sb$Parameter)
y <- s(p) # here the simulation happens

Uncertainty quantification: Sample the posterior distribution

For details on how to sample from the posterior distribution, see, e.g., the deterministic AKAR4 example. First we construct the prior:

sd <- rep(2,length(p))
dprior <- dNormalPrior(p,sd)
rprior <- rNormalPrior(p,sd)
llf <- logLikelihoodFunc(ex)
#> experiments contain 675 non-missing values
metropolis_hastings <- mcmcUpdate(s,ex,logLikelihood=llf,dprior=dprior)
MH_MCMC <- mcmc(metropolis_hastings)

We obtain a high quality sample by following the steps described in details in the deterministic AKAR4 example). This will take a minute or so on a laptop.

A <- function(a) {
    return(0.5 + a^4/(0.25^4 + a^4))
}

set.seed(137)
h <- 5e-2
N <- 3e4

nCores <- parallel::detectCores()
bigSample <- parallel::mclapply(
    seq(nCores),
    \(i) {
        x <- mcmcInit(
            1.0,
            parMCMC=t(rprior(1)),
            simulate=s,
            logLikelihood=llf,
            dprior=dprior)
        ## adjust acceptance rate to 25% via step-size h
        for (i in seq(30)){
            z <- MH_MCMC(x,200,h)
            x <- attr(z,"lastPoint")
            h <- h*A(attr(z,"acceptanceRate"))
        }
        return(MH_MCMC(x,N,h))
    },
    mc.cores=nCores
)

S_ <- Reduce(\(a,b) {rbind(a,b)},bigSample,init=NULL)
L_ <- Reduce(\(a,b) {c(a,attr(b,"logLikelihood"))},bigSample,init=NULL)
colnames(S_) <- names(p)

if (require(hexbin)){
    hexbin::hexplom(S_)
} else {
    pairs(S_)
}
#> Loading required package: hexbin

Sensitivity analysis on the posterior distribution

First we need to (re-)create the simulation result corresponding to the posterior parameter sample. This will take a minute or so on a laptop.

s <- simcf(ex,modelName,parMap=log10ParMap) # or simulator.c
y <- s(t(S_[,]))

Next we calculate the first order sensitivity indexes. Here for compute them for a specific experimental setting and time point:

E <- 2                      # Experiment idx
T <- 60                     # Time idx
fM <- y[[E]]$state[,T,]
SIappr <- gsa_binning(S_, t(fM), nBins = "Sturges")

and plot the result:

cols=rainbow(3)
par(mfrow = c(1, 1))
fM <- y[[E]]$state[,T,]
barplot(t(SIappr),
        col=cols,
        border="white",
        space=0.04,
        cex.axis=0.7,
        legend.text=sb$Parameter[,1])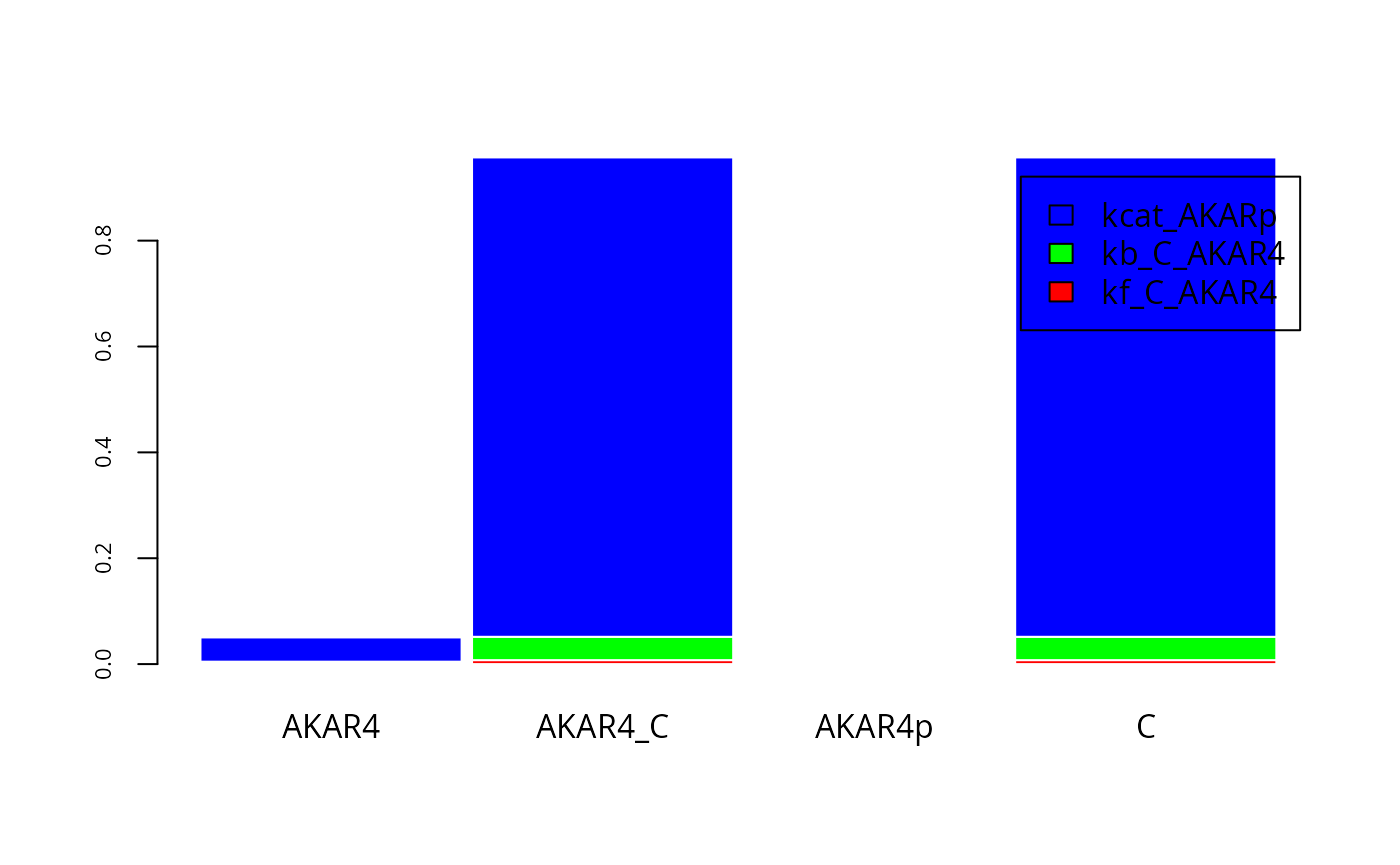

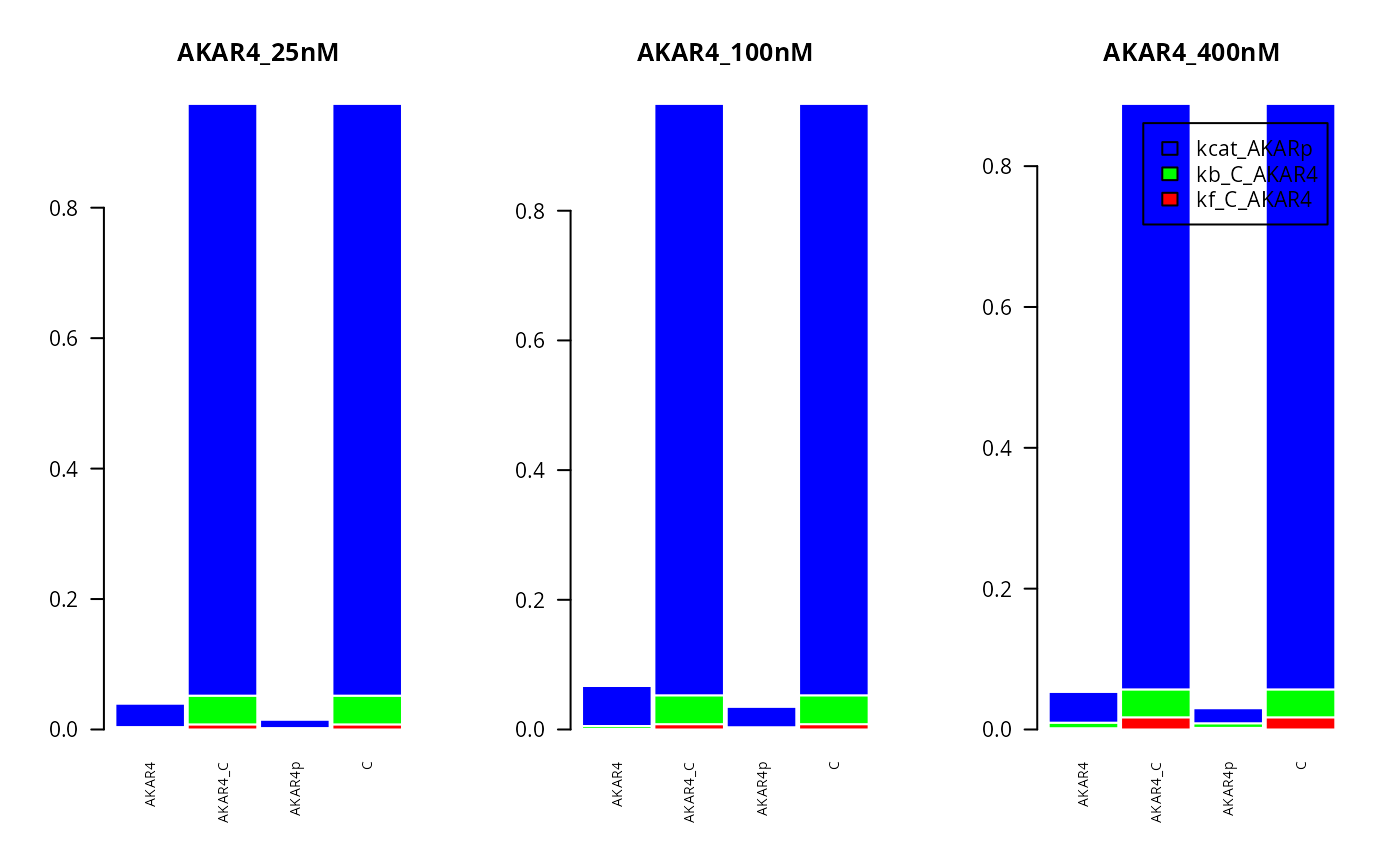
Here for compute the first order sensitivity indexes for all three experiments, looking at the different compounds in the system (on the x axis):

T <- 200                    #Time idx
par(mfrow = c(1, 3))
for (E in 3:1){
fM <- y[[E]]$state[,T,]
SIappr <-gsa_binning(S_, t(fM) , nBins = "Sturges")
lgd <- list(sb$Parameter[,1], NULL,NULL)
barplot(t(SIappr),
        col=cols,
        cex.names = 0.7,
        las=2,
        border="white",
        space=0.04,
        cex.axis=1,
        main=names(ex)[E],
        legend.text=lgd[[E]])
}

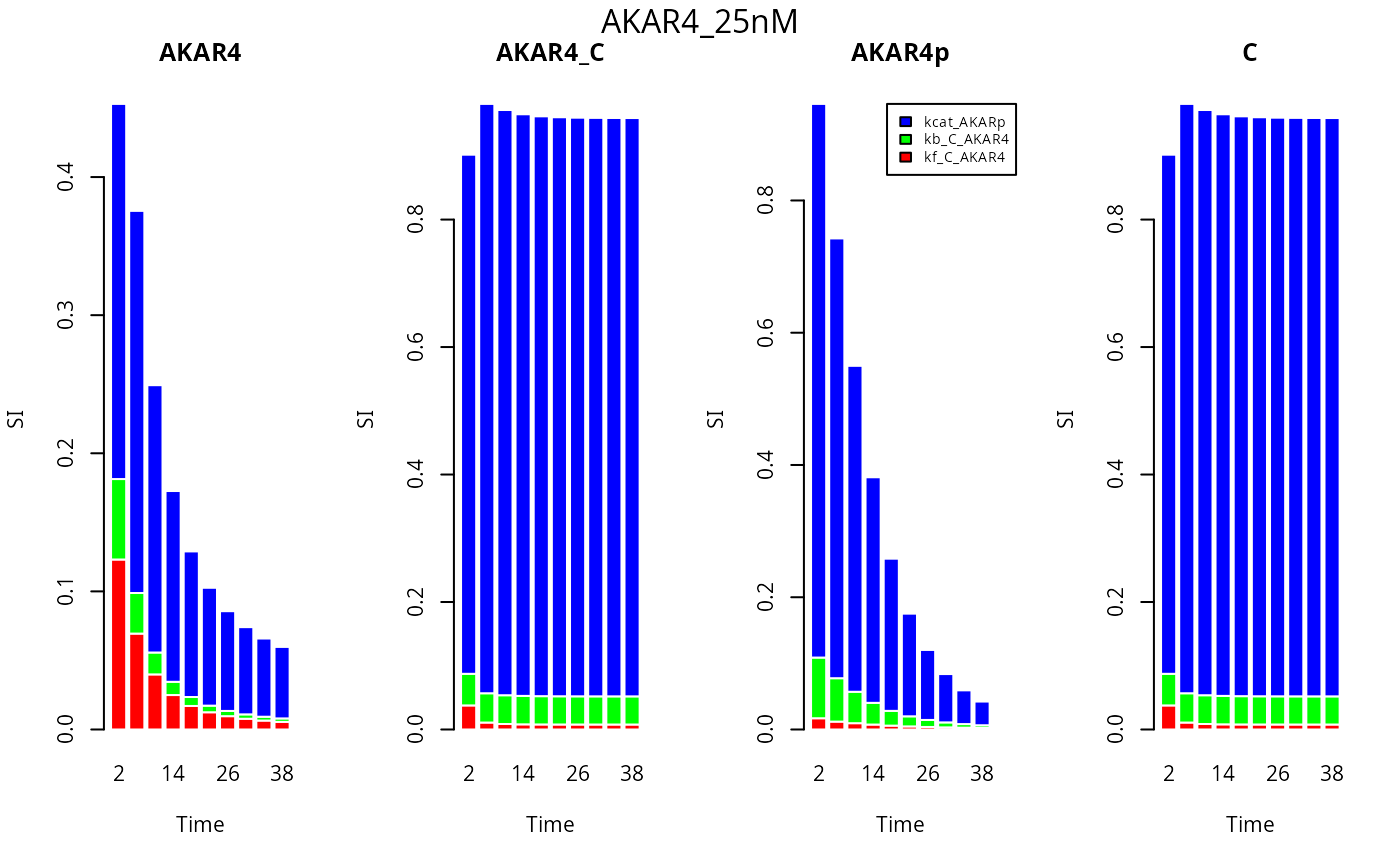
Now we investigate the first order sensitivity indexes at different time points (time is on the x axis) for each of the compounds and one experiment.

E <- 3
timePts <- seq(2,40,by=4)  #Avoid first time point
nStates=dim(y[[E]]$state)[1]
cols=rainbow(3)
par(mfrow = c(1, nStates))
lgd <- rep(list(NULL),nStates)
lgd[[nStates-1]] <- sb$Parameter[,1]
for (Cm in 1:nStates) {
  fM <- y[[E]]$state[Cm,timePts,]
  SIappr <-gsa_binning(S_, t(fM) , nBins = "Sturges")
  names(SIappr) <- timePts
  barplot(t(SIappr),
          col=cols,
          names.arg = timePts,
          border="white",
          cex.axis=1,
          main=dimnames(y[[E]]$state)[[1]][Cm],
          xlab="Time",
          ylab="SI",
          legend.text=lgd[[Cm]],
          args.legend = list(x = "topright", inset=c(-0.1, 0), cex=0.7)
          )
}
mtext(names(ex[E]), side=3, line = - 1.5,outer=TRUE)