Skip to contents

Importing Models into R

models.Rmd

If the model can be described in terms of reactions, inputs, and outputs, then the most straightforward way to define it is through SBtab tables.1 2

The following R commands load the SBtab model and data into R as data.frames, and convert the model into an ODE. First, you will need to get to the directory with the SBtab files by the command setwd(...).

f <- dir(pattern="[.]tsv$",full.names=TRUE)          # file names
sb <- SBtabVFGEN::sbtab_from_tsv(f)                  # a list of data.frames
ml <- SBtabVFGEN::sbtab_to_vfgen(sb)                 # ODE model (as a list)
ex <- SBtabVFGEN::sbtab.data(sb,ml$conservationLaws) # includes the data
C <- uqsa::generateCode(ml)                          # C Code
cat(C, sep = "\n", file = "AKAR4cl_gvf.c")

Some of the R commands above belong to our external package SBtabVFGEN.

More information on the R commands used in the previous code block, and further instructions on building and simulating your own model can be found in the pages “Build and simulate your own model” and “Importing Data”.

The rest of this page describes the variables and the files that we just created through the previous R commands.

Real Example 

library(uqsa)
library(SBtabVFGEN)

f <- uqsa_example('AKAR4')                           # file names
print(f[1])
sb <- SBtabVFGEN::sbtab_from_tsv(f)                  # a list of data.frames
cl <- SBtabVFGEN::sbtab_to_vfgen(sb)                 # conservation laws, if any
ex <- SBtabVFGEN::sbtab.data(sb,cl)                  # includes the data

The ex variable holds simulation instructions for the different experiments as an R list that includes information on inputs, initial values, measurement times, etc., and also the actual data.

SBtab content:

## Reactions, as an example of SBtab in R:
print(sb$Reaction)
#>                 !Name                             !KineticLaw
#> reaction_1 reaction_1 kf_C_AKAR4*C*AKAR4 - kb_C_AKAR4*AKAR4_C
#> reaction_2 reaction_2                      kcat_AKARp*AKAR4_C
#>                  !ReactionFormula !IsReversible
#> reaction_1  C + AKAR4 <=> AKAR4_C             1
#> reaction_2 AKAR4_C <=> AKAR4p + C             0
## Conservation Laws, as text, and its attributes:
cl$Text
#> [1] "AKAR4_C_ConservedConst = AKAR4_C+1*C"     
#> [2] "AKAR4_ConservedConst = AKAR4+1*AKAR4p-1*C"
## data:
head(ex[[1]]$outputValues)
#>          AKAR4pOUT
#> E400T001    108.60
#> E400T002    111.35
#> E400T003    108.75
#> E400T004    111.40
#> E400T005    111.70
#> E400T006    113.25
head(ex[[1]]$errorValues)
#>          AKAR4pOUT
#> E400T001   14.7950
#> E400T002   14.9325
#> E400T003   14.8025
#> E400T004   14.9350
#> E400T005   14.9500
#> E400T006   15.0275

Data as a plot:

i <- seq(70)
t <- ex[[1]]$outputTimes[i]
y <- ex[[1]]$outputValues[[1]][i]
dy <- ex[[1]]$errorValues[[1]][i]
plot(t,y,bty='n',ylim=c(100,200))
arrows(t,y,t,y+dy,angle=90, length=0.01)
arrows(t,y,t,y-dy,angle=90, length=0.01)

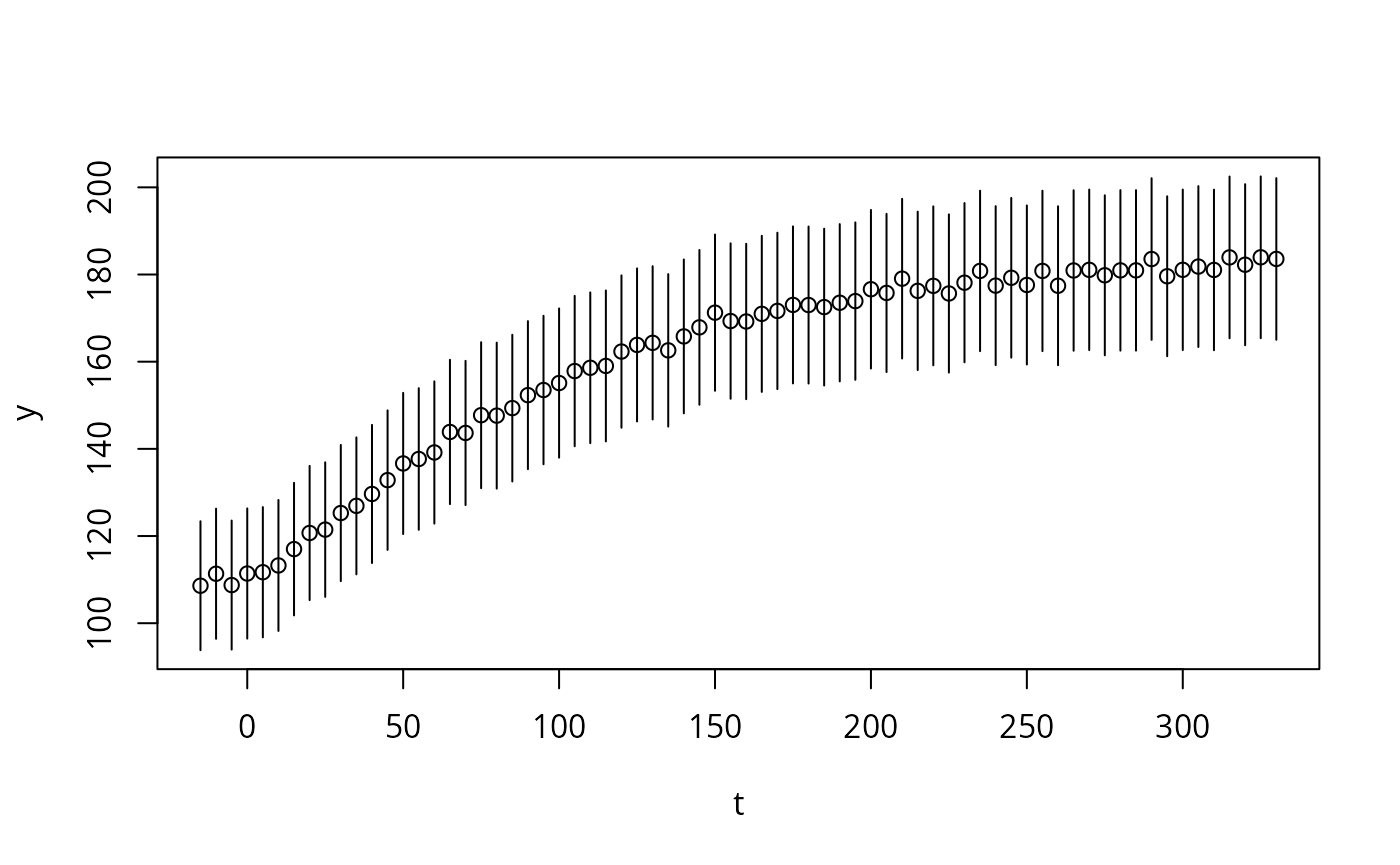
Files

The function sbtab_to_vfgen will produce several files, with the model’s name (Document='model_name' attribute of SBtab) and different extensions:

  • model_name.vf, a vfgen compatible file
  • model_name.mod, a NEURON mod file
  • (optional) model_name.xml, an SBML file, if you have the R bindings to libsbml installed in R and libsbml in your system
  • model_name.tar.gz, compressed archive of a text representation of all ODE elements, no specific format
  • model_name.zip, the same as tar.gz, but as a zip archive

Let’s look at the state variables of the ode:

grep '<StateVariable' AKAR4.vf
#> <!-- <StateVariable Name="AKAR4" Description="removed compound" DefaultInitialCondition="0.2" Formula="-reaction_1"/> -->
#> <!-- <StateVariable Name="AKAR4_C" Description="removed compound" DefaultInitialCondition="0" Formula="+reaction_1-reaction_2"/> -->
#>  <StateVariable Name="AKAR4p" Description="compound" DefaultInitialCondition="0" Formula="+reaction_2"/>
#>  <StateVariable Name="C" Description="compound" DefaultInitialCondition="0" Formula="-reaction_1+reaction_2"/>

Two State variables have been commented out (through conservation law analysis). These two have been replaced by vfgen expressions:

grep '<Expression' AKAR4.vf
#>  <Expression Name="AKAR4_C" Description="derived from conservation law 1" Formula="AKAR4_C_ConservedConst - (C)"/>
#>  <Expression Name="AKAR4" Description="derived from conservation law 2" Formula="AKAR4_ConservedConst - (AKAR4p-C)"/>
#>  <Expression Name="reaction_1" Description="flux" Formula="kf_C_AKAR4*C*AKAR4 - kb_C_AKAR4*AKAR4_C"/>
#>  <Expression Name="reaction_2" Description="flux" Formula="kcat_AKARp*AKAR4_C"/>

Finally, we clean up the generated files:

for t in vf tar.gz zip ; do rm ./AKAR4.$t ; done
[ -f AKAR4.xml ] && rm AKAR4.xml # since that one is optional
echo $?

The Vector Field file

The vf file is compatible with the vfgen tool, which creates code in many languages from this vf file (MATLAB, CVODE, Octave, Python, XPPAUT). Use this tool if you want to use the created source code for other programming languages. Some SBtab content will be missing here (e.g., scheduled events). The vfgen tool uses the GiNaC library to calculate Jacobians. GiNaC cannot parse vf files with inequality expressions in them (e.g. a < b).

Converting the ODE to code

We use our tool, RPN-derivative, which reads the same file (or one of the archive files: zip/tar.gz) to create slightly different C code. The main advantages are:

  • a vector valued output function with a predictable name: int MODEL_func()
  • the error code of each function is the length of the output buffers that need to be allocated
  • more functions are created:
    • initial conditions: int MODEL_init()
    • default parameter values: int MODEL_default()

The repository of this tool, icpm-kth/RPN-derivative, contains a shell script ode.sh; this script uses one of three methods to calculate analytical derivatives for the Jacobians: 1. maxima, 2. yacas, 3. the bin/derivative binary that RPN-derivative contains (after make && make install)

Assuming that you followed all installation instructions:

ode -R --maxima ./myModel.vf > ./myModel.R 
##     both     ./myModel.{zip,tar.gz}     also work here
ode -C --maxima ./myModel.tar.gz > ./myModel_gvf.c

Note: ode.sh is compatible with the same vf files from SBtabVFGEN, but doesn’t support all of the output formats that VFGEN can do, and does nothing related to delays.

Background on Parameters vs Inputs

Our goal is to perform parameter estimation. A systems biology model typically has parameters that are either reaction rate coefficients \(k_f, k_b\), equilibrium constants \(K_d\), Hill coefficients, and many other quantities related to kinetc laws. Parameters are often unknown or not uniquely determined yet. However, not all parameters of a model are unknown, and not all parameters are intrinsic to the system we study. Some of them describe the interventions we do to the system when performing an experiment. This could be the frequency of a driving force for a mechanical model, or the amount of a treatment dose (added to the system) that affects the time course of reactions:

  • a substrate, or buffer
  • an enzyme,
  • a silencing agent,
  • an inhibitor

These parameters are known to us, because they are written down in the protocol. If the input is time dependent, then its dynamics (or explicit algebraic functions) have to become part of the model. These input parameters can be different between experiments, but the intrinsic parameters (e.g., reaction rate coefficients) are always the same.

The ordinary differential equation, on the other hand, does not need to know the distinction between known or unknown parameters. For these reasons, we may write:

parMCMC <- [...]             # some sampling variable
k <- parMap(parMCMC)         # a model compatible parameter vector
u <- experiments[[i]]$input  # a valid model input vector
p <- c(k,u)
# solve ODE using p

where k are intrinsic, unknown parameters (of which we quantify the uncertainty via sampling algorithms in UQSA), and u are the known input parameters that are encoded in the input field of an experiment.

If input parameters u exist, then they are always concatenated (p <-c(k,u)) in that order (after intrinsic, unknown parameters) and passed to the model. The model’s C code only sees p. The wrapper functions in the rgsl package do this concatenation when the solver is called. We sample in logarithmic space, but the solver gets k and appends the right u for each experiment, both in linear space.

So, if parMCMC is in log10-space, then parMap is the transformation to linear-space for the solver to work in:

parMap <- function(par) {
    return(10^(par))
}