ODE Model • uqsa

In some cases, the model already is an Ordinary Differential Equation, and we don’t want to first think of it as a reaction network.

In such cases, these approaches are equally good/plausible:

write the model in vfgen’s vf format
- avoid line-breaks in self-closed tags: <SomeElement attr="value"/> (always one line)
- ode.sh does not use an xml parser since there is no mathml
- The attribute values are extracted using regular expressions and POSIX tools
- standard regular expressions usually don’t deal well with content that is spread across lines (Rob Pike wrote about this a long time ago)
use the ode format of xpp and xppaut
- there is limited support for this format as xpp has a huge list of capabilities
- differentiation has to be var' = formula, with a ' (prime)
- no delay equations
- no DAE
- no bdry, global, wiener, table, and other special functions
convert the model into the text form used by RPN-derivative/sh/ode.sh, by imitating the examples
- ode.sh has an --inspect option that leaves the created temporary files intact for inspection
- this can be used for debugging as well
- whichever format ode.sh receives, it will convert everything into txt files that end up in the temp folder
- on GNU/Linux the temp folder is /dev/shm/ode_gen/ (it doesn’t survive reboots)
write the model’s C source code directly using a computer algebra system
- maxima and yacas are good
- this is not automated at all
- feasible if you have experience with these tools

On this page, we will use the .ode method.

Simple Example

Let’s take this model of a pendulum as an example, in xpp’s .ode format because it is very compact and beautiful:

# pendulum.ode
par g=9.81
par b=0.0
par L=1.0
par m=1.0

theta'=v
init theta=3.13159

v'=-v*m^(-1)*b*L^(-2)-g*sin(theta)*L^(-1)
init v=0.0

# Output
aux energy=-m*g*cos(theta)*L+0.5*v^2*m*L^2
#
done

We will use this model, and convert it to the text format that ode.sh can read using standard command line tools:

f="pendulum.ode"
echo "$f"
egrep '^par' "$f" | tr '=' '\t' | sed 's/^par //' > Parameters.txt
egrep '^init' "$f" | tr '=' '\t' | sed 's/^init //' > StateVariables.txt
egrep "'" "$f" | sed -E "s/([^=]*)'=/\1\t/;" > ODE.txt
egrep '^aux' "$f" | tr '=' '\t' | sed 's/^aux[ ]*//' > OutputFunctions.txt
tar czf pendulum.tar.gz Parameters.txt StateVariables.txt ODE.txt OutputFunctions.txt
[ -f pendulum.tar.gz ] && ode -C --maxima pendulum.tar.gz > pendulum_gvf.c

At this stage, we could add transformations (manually), if we wanted.

But, actually, there is a limited parser for ode files that does something like the above. It runs if the model file ends in ode:

ode -C --maxima pendulum.ode > pendulum_gvf.c
#> -C --maxima pendulum.ode
#> Operating on these files:
#> CON «/dev/shm/ode_gen/Constants.txt»
#> PAR «/dev/shm/ode_gen/Parameters.txt»
#> VAR «/dev/shm/ode_gen/StateVariables.txt»
#> EXP «/dev/shm/ode_gen/Expressions.txt»
#> FUN «/dev/shm/ode_gen/OutputFunctions.txt»
#> ODE «/dev/shm/ode_gen/ODE.txt»
#> EVT «/dev/shm/ode_gen/Transformations.txt»
#> 2 state variables, 4 parameters, 0 expressions, 1 functions
#> y-jacobian df[i]/dy[j] has size 4 (2×2)
#> p-jacobian df[i]/dp[j] has size 8 (2×4)

The resulting code can be found at the bottom of this page.

In R, we can use this code directly:

library(rgsl)
library(uqsa)

f <- "pendulum_gvf.c"
modelName <- checkModel("pendulum",f)
#> building a shared library from c source, and using GSL odeiv2 as backend (pkg-config is used here).
#> cc -shared -fPIC `pkg-config --cflags gsl` -o './pendulum.so' 'pendulum_gvf.c' `pkg-config --libs gsl`

ex <- list(
    test=list(
        initialTime=-1.0,
        outputTimes=seq(0,10,0.1))
    )

SIM <- simcf(ex,modelName)
par <- c(g=9.81, b=0.0, L=1.0, m=1.0)
print(par)
#>    g    b    L    m 
#> 9.81 0.00 1.00 1.00

y <- SIM(par)
plot(ex[[1]]$outputTimes,y[[1]]$state[1,,1],xlab='t',ylab='theta',bty='n',type='l')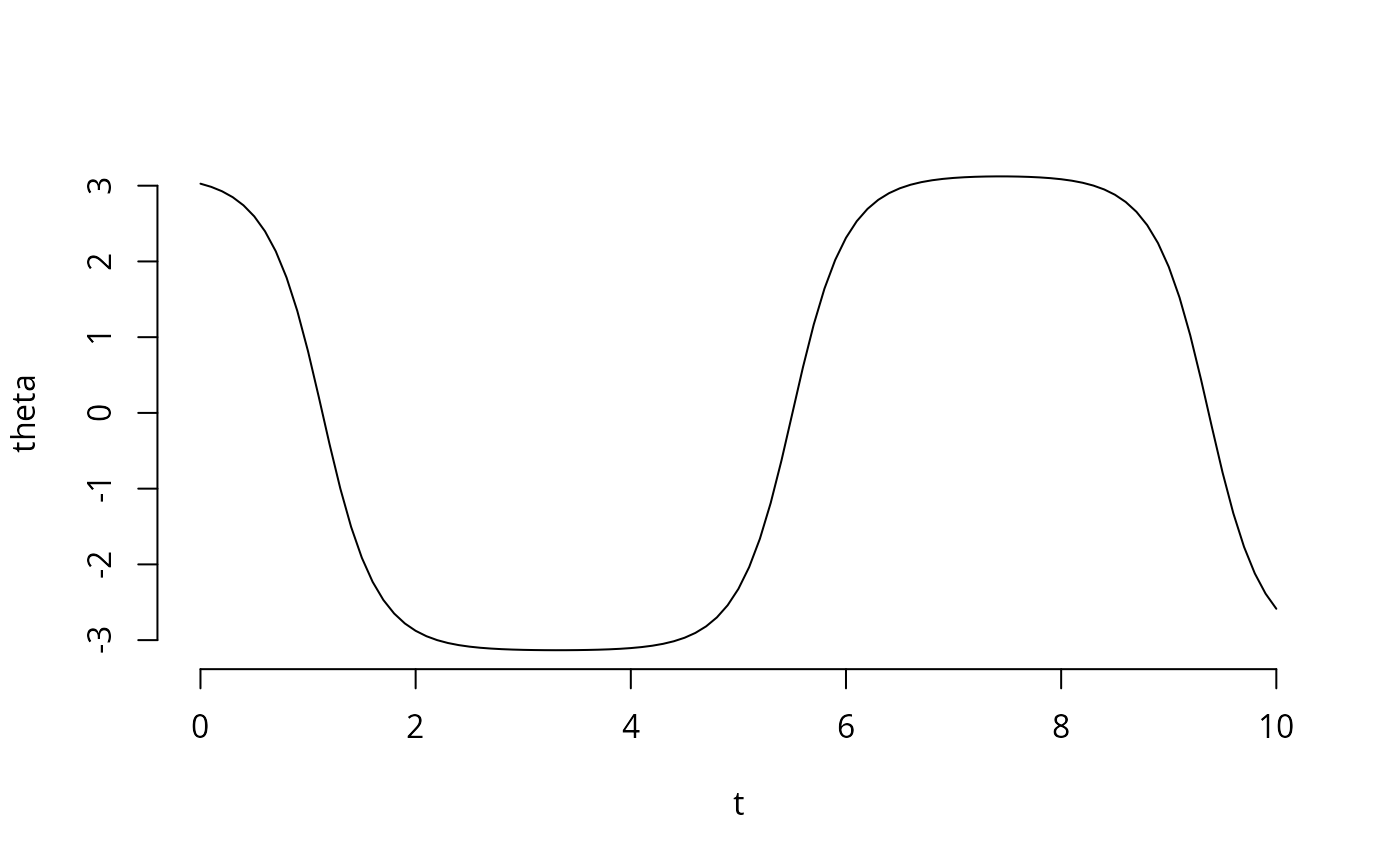

Generated C Code

#include <stdlib.h>
#include <math.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_odeiv2.h>
#include <gsl/gsl_math.h>

enum stateVariable { _theta,_v, numStateVar }; /* state variable indexes  */
enum param { _g,_b,_L,_m, numParam }; /* parameter indexes  */
enum func { _energy, numFunc }; /* parameter indexes  */

/* The error code indicates how to pre-allocate memory
 * for output values such as `f_`. The _vf function returns
 * the number of state variables, if any of the args are `NULL`.
 * evaluation errors can be indicated by negative return values.
 * GSL_SUCCESS (0) is returned when no error occurred.
 */

/* ode vector field: y'=f(t,y;p) */
int pendulum_vf(double t, const double y_[], double f_[], void *par)
{
    double *p_=par;
    if (!y_ || !f_) return 2;
    double g=p_[0];
    double b=p_[1];
    double L=p_[2];
    double m=p_[3];
    double theta=y_[0];
    double v=y_[1];
    f_[_theta] = v; /* theta */
    f_[_v] = -v*pow(m,-1)*b*pow(L,-2)-g*sin(theta)*pow(L,-1); /* v */
    return GSL_SUCCESS;
}
/* ode Jacobian df(t,y;p)/dy */
int pendulum_jac(double t, const double y_[], double *jac_, double *dfdt_, void *par)
{
    double *p_=par;
    if (!y_ || !jac_) return 2*2;
    double g=p_[0];
    double b=p_[1];
    double L=p_[2];
    double m=p_[3];
    double theta=y_[0];
    double v=y_[1];
/* column 1 (df/dy_0) */
    jac_[0] = 0; /* [0, 0] */
    jac_[2] = -(g*cos(theta))/L; /* [1, 0] */
/* column 2 (df/dy_1) */
    jac_[1] = 1; /* [0, 1] */
    jac_[3] = -b/(gsl_pow_2(L)*m); /* [1, 1] */
    return GSL_SUCCESS;
}
/* ode parameter Jacobian df(t,y;p)/dp */
int pendulum_jacp(double t, const double y_[], double *jacp_, double *dfdt_, void *par)
{
    double *p_=par;
    if (!y_ || !jacp_) return 2*4;
    double g=p_[0];
    double b=p_[1];
    double L=p_[2];
    double m=p_[3];
    double theta=y_[0];
    double v=y_[1];
/* column 1 (df/dp_0) */
    jacp_[0] = 0; /* [0, 0] */
    jacp_[4] = -sin(theta)/L; /* [1, 0] */
/* column 2 (df/dp_1) */
    jacp_[1] = 0; /* [0, 1] */
    jacp_[5] = -v/(gsl_pow_2(L)*m); /* [1, 1] */
/* column 3 (df/dp_2) */
    jacp_[2] = 0; /* [0, 2] */
    jacp_[6] = (2*b*v)/(gsl_pow_3(L)*m)+(g*sin(theta))/gsl_pow_2(L); /* [1, 2] */
/* column 4 (df/dp_3) */
    jacp_[3] = 0; /* [0, 3] */
    jacp_[7] = (b*v)/(gsl_pow_2(L)*gsl_pow_2(m)); /* [1, 3] */
    return GSL_SUCCESS;
}
/* ode Functions F(t,y;p) */
int pendulum_func(double t, const double y_[], double *func_, void *par)
{
    double *p_=par;
    if (!y_ || !func_) return 1;
    double g=p_[0];
    double b=p_[1];
    double L=p_[2];
    double m=p_[3];
    double theta=y_[0];
    double v=y_[1];
    func_[_energy] = -m*g*cos(theta)*L+0.5*gsl_pow_2(v)*m*gsl_pow_2(L); /* energy */
    return GSL_SUCCESS;
}
/* Function Jacobian dF(t,y;p)/dy */
int pendulum_funcJac(double t, const double y_[], double *funcJac_, void *par)
{
    double *p_=par;
    if (!y_ || !funcJac_) return 2;
    double g=p_[0];
    double b=p_[1];
    double L=p_[2];
    double m=p_[3];
    double theta=y_[0];
    double v=y_[1];
/* column 1 (dF/dy_0) */
    funcJac_[0] = L*g*m*sin(theta); /* [0, 0] */
/* column 2 (dF/dy_1) */
    funcJac_[1] = 1.0*gsl_pow_2(L)*m*v; /* [0, 1] */
    return GSL_SUCCESS;
}
/* Function parameter Jacobian dF(t,y;p)/dp */
int pendulum_funcJacp(double t, const double y_[], double *funcJacp_, void *par)
{
    double *p_=par;
    if (!y_ || !funcJacp_) return 4;
    double g=p_[0];
    double b=p_[1];
    double L=p_[2];
    double m=p_[3];
    double theta=y_[0];
    double v=y_[1];
/* column 1 (dF/dp_0) */
    funcJacp_[0] = -L*m*cos(theta); /* [0, 0] */
/* column 2 (dF/dp_1) */
    funcJacp_[1] = 0; /* [0, 1] */
/* column 3 (dF/dp_2) */
    funcJacp_[2] = 1.0*L*m*gsl_pow_2(v)-g*m*cos(theta); /* [0, 2] */
/* column 4 (dF/dp_3) */
    funcJacp_[3] = 0.5*gsl_pow_2(L)*gsl_pow_2(v)-L*g*cos(theta); /* [0, 3] */
    return GSL_SUCCESS;
}
/* ode default parameters */
int pendulum_default(double t, void *par)
{
    double *p_=par;
    if (!p_) return 4;
    p_[_g] = 9.81;
    p_[_b] = 0.0;
    p_[_L] = 1.0;
    p_[_m] = 1.0;
    return GSL_SUCCESS;
}
/* ode initial values */
int pendulum_init(double t, double *y_, void *par)
{
    double *p_=par;
    if (!y_) return 2;
    double g=p_[0];
    double b=p_[1];
    double L=p_[2];
    double m=p_[3];
    /* the initial value of y may depend on the parameters. */
    y_[_theta] = 3.13159;
    y_[_v] = 0.0;
    return GSL_SUCCESS;
}